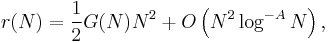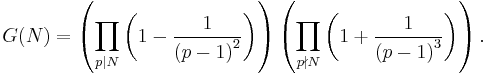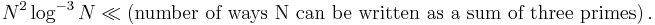Vinogradov's theorem
In number theory, Vinogradov's theorem implies that any sufficiently large odd integer can be written as a sum of three prime numbers. It is a weaker form of Goldbach's conjecture, which would imply the existence of such a representation for all odd integers greater than five. It is named after Ivan Matveyevich Vinogradov who proved it in the 1930s. The full statement of Vinogradov's theorem gives asymptotic bounds on the number of representations of an odd integer as a sum of three primes.
Contents |
Statement of Vinogradov's theorem
Let A be a positive real number. Then
where
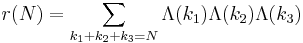 ,
,
using the von Mangoldt function 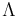 , and
, and
A consequence
If N is odd, then G(N) is roughly 1, hence 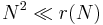 for all sufficiently large N. By showing that the contribution made to r(N) by proper prime powers is
for all sufficiently large N. By showing that the contribution made to r(N) by proper prime powers is 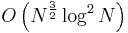 , one sees that
, one sees that
This means in particular that any sufficiently large odd integer can be written as a sum of three primes, thus showing Goldbach's weak conjecture for all but finitely many cases.
References
- I.M. Vinogradov (1954). The Method of Trigonometrical Sums in the Theory of Numbers. New York: Interscience.
- Melvyn B. Nathanson (1996). Additive Number Theory: the Classical Bases. Graduate Texts in Mathematics. 164. Springer-Verlag. ISBN 0-387-94656-X. Chapter 8.